ここに3本の棒が立っている。左端の棒には3枚の大きさの違う円盤が突き刺さっている。円盤は下から大中小の順になっている。
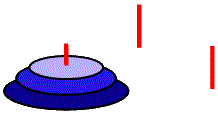
この3枚の円盤を別の棒に移し替えたいのだが、ルールがある。
- 棒から棒に動かす。
- 一度に動かせるのは1枚だけ。
- 下の円盤より大きな円盤を載せてはいけない。
さて、どうすればよいか。
円盤が3枚のとき、最短の作業回数は7回である。
棒は3本のまま、円盤を1枚増やし、4枚とすると、作業回数は15回となる。
一般に、円盤がn枚のときには、2n-1回の作業が必要である。
さて、これを証明してみよう。ここで、数学的帰納法を使う。
n=1が成立することを示す
まず、n=1のとき成立することを示す。
円盤1枚を別の棒に刺すだけだから、作業回数は1回。n=1のとき、2n-1=1である。よって示せた。
n=kが成立すると仮定し、n=k+1が成立することを示す
次に、n=kのとき成立すると仮定する。
今、円盤が位置Aにk+1枚ある。これを位置Cに移したい。
まず、上からk枚を位置Bに移す。n=kのとき成立しているのだから、ここまでの作業回数は2k-1回。
一番下のk+1枚目を位置Cに移す。この作業回数が1回。
位置Bにあるk枚を位置Cのk+1枚目の上に移すのは、位置Aから位置Bにk枚を移動させたのと同じことだから、ここでの作業回数は2k-1回。
これらの一連の作業回数は2k-1+1+2k-1=2k+2k-1=2*2k-1=2k+1-1
つまりk+1枚を移すのに2k+1-1回の作業が必要であった。
言い換えると「n=k+1のときに2n-1回の作業が必要である」ということが正しいことが示された。
解法
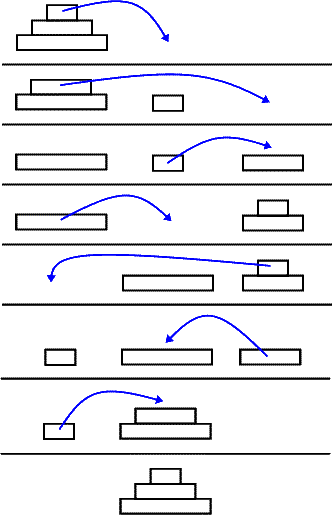




コメント