 小ネタ
小ネタ 曲線に接する円の中心の描く軌跡は元の曲線とずれる
YouTubeで板を切る動画がありました。元の板の曲線に沿って別の板を切るときに、円(ワッシャーなど)を当てて中心で線を描いています。元の曲線から最短距離の曲線が描けます。動画では切断したところが元の曲線にぴったり合っているように見えますが...
 小ネタ
小ネタ  豆知識
豆知識  小ネタ
小ネタ  Python
Python  Tool
Tool 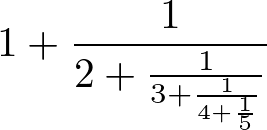 Python
Python  豆知識
豆知識 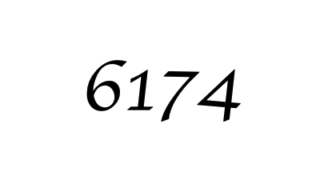 豆知識
豆知識  Python
Python  JavaScript
JavaScript