a+ar+ar2+ar3+ar4+…+arn=a(1-rn+1)/(1-r)
という公式がある。aを初項、rを等比という。
これを利用して、
Σ2k=2+4+8+16+…+2n
がどうなるかを調べたい。これはいわゆる等比級数のようだが、初項2、等比2と考えてしまうと少し違う。
初項2、等比2の等比級数は
2+2*2+2*22+…+2*2n-1+2*2n=2+4+8+ +2n+2n+1
最後の「+2n+1」が余分である。
一方、公式を使うと初項2、等比2の等比級数は2*(1-2n+1)/(1-2)=2*(2n+1-1)となる。
したがって、2+4+8+…+2n+2n+1=2*(2n+1-1)
余分な「+2n+1」を右辺に移項すると、
2+4+8+…+2n=2*(2n+1-1)-2n+1=2n+1-2
よって、Σ2k=2n+1-2
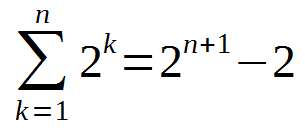



コメント
[…] となる(「2のn乗までの和」を参照)。一方、 […]