Microsoft Researchが作ったZ3というツールがあります。
これを使うと魔方陣や数独などを簡単に解くことができます。
簡単にと言っても使い方は難しいです。
今回はPythonでZ3を使って覆面算を解いてみます。Macで試しました。
Z3のインストール
$ pip install z3-solver
問題

send+more=moneyという有名な覆面算です。
各文字には0から9までの整数が入ります。
同じ文字には同じ数が入り、異なる文字には異なる数が入ります。
計算が成り立つように各文字に何が入るかを求めます。
コード
from z3 import *
# 変数の作成
s, e, n, d, m, o, r, y = Ints(["s", "e", "n", "d", "m", "o", "r", "y"])
# ソルバのインスタンスを生成
slv = Solver()
# 制約 異なる値を持つ
slv.add(Distinct([s, e, n, d, m, o, r, y]))
# 制約 1以上9以下
slv.add(1 <= s, s <= 9)
slv.add(0 <= e, e <= 9)
slv.add(0 <= n, n <= 9)
slv.add(0 <= d, d <= 9)
slv.add(1 <= m, m <= 9)
slv.add(0 <= o, o <= 9)
slv.add(0 <= r, r <= 9)
slv.add(0 <= y, y <= 9)
# 制約 計算
slv.add(s * 1000 + e * 100 + n * 10 + d * 1 + m * 1000 + o * 100 + r * 10 + e * 1 == m * 10000 + o * 1000 + n * 100 + e * 10 + y * 1)
result = slv.check()
if result == sat:
mdl = slv.model()
print(mdl)
print("send", mdl[s], mdl[e], mdl[n], mdl[d])
print("more", mdl[m], mdl[o], mdl[r], mdl[e])
print("money", mdl[m], mdl[o], mdl[n], mdl[e], mdl[y])
else:
print(result)
# 変数の作成
s, e, n, d, m, o, r, y = Ints(["s", "e", "n", "d", "m", "o", "r", "y"])
# ソルバのインスタンスを生成
slv = Solver()
# 制約 異なる値を持つ
slv.add(Distinct([s, e, n, d, m, o, r, y]))
# 制約 1以上9以下
slv.add(1 <= s, s <= 9)
slv.add(0 <= e, e <= 9)
slv.add(0 <= n, n <= 9)
slv.add(0 <= d, d <= 9)
slv.add(1 <= m, m <= 9)
slv.add(0 <= o, o <= 9)
slv.add(0 <= r, r <= 9)
slv.add(0 <= y, y <= 9)
# 制約 計算
slv.add(s * 1000 + e * 100 + n * 10 + d * 1 + m * 1000 + o * 100 + r * 10 + e * 1 == m * 10000 + o * 1000 + n * 100 + e * 10 + y * 1)
result = slv.check()
if result == sat:
mdl = slv.model()
print(mdl)
print("send", mdl[s], mdl[e], mdl[n], mdl[d])
print("more", mdl[m], mdl[o], mdl[r], mdl[e])
print("money", mdl[m], mdl[o], mdl[n], mdl[e], mdl[y])
else:
print(result)
結果
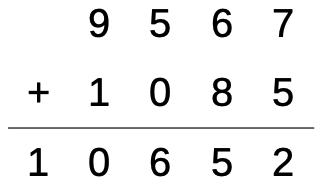
[r = 8, s = 9, e = 5, d = 7, n = 6, o = 0, m = 1, y = 2]
send 9 5 6 7
more 1 0 8 5
money 1 0 6 5 2
説明
変数を作ります。Intsは整数であることを示します。
ソルバのインスタンスを作ります。
制約条件を列挙します。
addを使って制約をどんどん追加していきます。
Distinctを使うと配列内の変数が異なる値であることを示します。
数の範囲の条件を指定します。Pythonでは通常は「a<x<b」という書き方ができますが、ここではできません。左端の数はゼロにならないので「s」と「m」だけは1以上としています。
計算の条件を指定します。
条件に合致するものを探す問題を充足可能性問題、SATと呼びます。
checkを使ってSATに該当するかチェックします。
該当する場合は解けます。


コメント