私がよく行くスーパーはレジ袋が有料です。
その代わり、使用済みの段ボールをくれます。段ボールは折り畳まれた状態で置かれています。なるべく容量の多い物を使いたいです。
そこでこんなことを考えてみました。
折り畳んだ状態の大きさが同じ場合、容量が最大になるのはどんな段ボールか。
変動する要因としては「縦と横の比」、「縦と箱の高さの比」が考えられます。
ここでは「縦と横の比」をwとして固定、「縦と箱の高さの比」をxとして、容量が最大となるときのxの値を求めます。

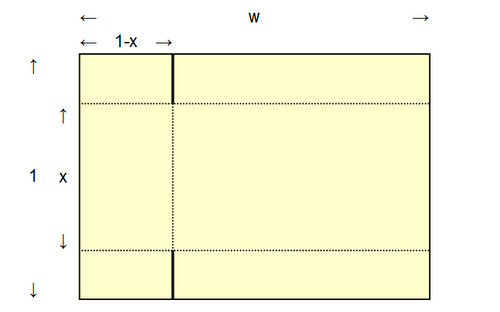
折り畳まれた段ボールの縦を1、横をwとする。
段ボール箱に組み立てたときの高さをxとする。
箱の幅は1-x、箱の奥行きはw-1+xとなる。
体積は箱の高さ、幅、奥行きの積なので
V=x(1-x)(w-1+x)
となる。
これをxの関数としてVが最大となるxを求める。
微分すると
V’=-3x^2+2(-w+2)x+w-1
となる。これが0となるxを求める。xの2次方程式として解くと
![]()
となる。
畳んだ状態の段ボールの横が縦の2倍のときを考えます。
w=2となるので代入するとx=0.577となります。
同様に
w=1.5のときx=0.607
w=1のときx=0.667
となります。
通常の段ボールは横が縦の1倍から2倍の間に収まるでしょうから、xは概ね0.6となります。
つまり、ベロの部分が0.2の割合ならば容量が最大になります。
実際にはペットボトルなどが入る縦長の箱が該当します。
野菜などが入る横長の箱は段ボールのサイズの割には容量が少ないです。



コメント