あらかじめ用意しておいた言葉をランダムに表示させる場合は乱数を使います。JavaScriptの場合です。
ws=["大吉","吉","末吉","凶","大凶"];
i=Math.floor(Math.random()*5);
alert(ws[i]);
i=Math.floor(Math.random()*5);
alert(ws[i]);
乱数はMath.random()で得ます。0から1までの間の数が返ります。
したがって大吉から大凶までの5種類に振り分けるためには5倍して端数を切り捨てることで0,1,2,3,4の整数を得ます。
この場合、0から4までの整数が均等に出ます。
「大吉が5分の1なのは少なすぎる。2分の1にしてほしい」となった場合のやり方を考えます。
次のような関数「bias」を作ります。
確率rについては値s以下が返り、確率(1-r)については値s超が返ります。
例えばr=0.5、s=0.2とすると、確率1/2については0.2以下の値(0<=値<=0.2)が返ります。上の例ではこれが「大吉」に相当します。
残りの1/2については0.2超の値(0.2<値<1.0)が返ります。0.2から1.0までは均等な値が返ります。上の例では「吉」から「大凶」までに相当します。
ws=["大吉","吉","末吉","凶","大凶"];
i=Math.floor(bias(Math.random(),0.5,0.2)*5);
alert(ws[i]);
function bias(num, r, s){
//値s以下となる確率をrとする。
if(num < r){
b = num * (1 / r) * s;
}else{
b = s + (num - r) / (1 - r) * (1 - s);
}
return(b);
}
i=Math.floor(bias(Math.random(),0.5,0.2)*5);
alert(ws[i]);
function bias(num, r, s){
//値s以下となる確率をrとする。
if(num < r){
b = num * (1 / r) * s;
}else{
b = s + (num - r) / (1 - r) * (1 - s);
}
return(b);
}
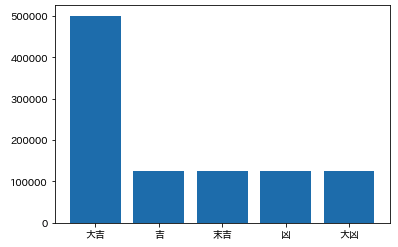
次は、100万回、実行した結果です。
大吉 500364
吉 124692
末吉 125084
凶 124937
大凶 124923


コメント
はじめましてこんにちは
大変参考にさせていただいてます。
当方javascriptの初心者なのですが、
b = num * (1 / r) * s;
}else{
b = s + (num – r) / (1 – r) * (1 – s);
上記2つの計算のそれぞれは確率論?みたいな数学的方程式を利用した計算なのでしょうか?
数学的見地があまりにもないので教えて頂けると嬉しいです。
お手数ですが宜しくお願いします。
あゆみさん
数学の確率の問題です。
公式はないと思います。自分で導きました。
数学でもJavaScriptでもご質問があれば分かる範囲でお答えします。