立方体の切断問題
立方体の切断問題というのがあります。よくあるのが「3点を通る面で立方体を切断せよ」という問題です。
例えば次のような問題です。
指定された3点を通るように立方体を切断し、その際の切断線を描いてください。辺にある点は中点(辺のちょうど中間の点)とします。
解き方
立方体をある面で切断したときにできる図形を「切断面」と呼ぶことにします。また、切断面の辺を「切断線」、頂点を「切断点」と呼ぶことにします。
基本的な考え方は次の二つです。
- 二つの点が同一面にあれば直線で結ぶ。
- 向かい合う面にある直線は平行になる。
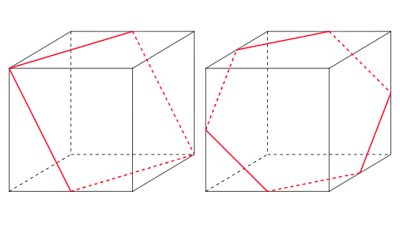
ほとんどはこの二つで解けますが、まれに点が同一面にない場合があります。この場合は切断面が六角形になることが多いです。なお、これは経験的にそうであるというだけで証明したわけではありません。
それでは解いてみます。まず上面に注目します。同一面にある2点は結べます。
上面に直線があり、下面に点がありますので、下面に直線が描かれるはずです。上面と下面は向かい合っていますので、上面の直線と下面の直線は平行になります。上面に切断線と二つの辺でできる直角三角形があります。二つの辺の長さは2:1になっていることに注目し、これと合同になる直角三角形を下面に描くと考えるとよいでしょう。
手前面の下の辺が切断線と交わりました。左上の点と切断点は同一面にありますので結べます。
手前面に切断線があるので奥面にこれと平行になる切断線があるはずです。奥面の切断点を通るように切断線を描きます。手前面に切断線と二つの辺でできる直角三角形があります。二つの辺の長さは4:3になっていることに注目し、これと合同になる直角三角形が奥面にあると考えるといいでしょう。
最後に、右面に切断点が二つあるので、これを結びます。

コメント