こんな問題がありました。
3枚のカードが袋に入っています。
1枚は両面赤(A)、1枚は両面青(B)、1枚は片面が赤で片面が青(C)です。
今、目をつぶって袋からカードを1枚選び、机の上に置いて目を開けたところ、カードは赤でした。
このカードの裏が青である確率は?
「赤が出たということはAかCの2枚。その反対が青であるのはC。2通りのうち1通りなので確率は1/2」と考える人が多いようです。
しかし違います。
「条件付き確率」と言われる、この手の確率の問題はまず最初に起きうるパターンを列挙すると分かりやすいです。
3枚のカードを次のように考えます。
A 表:赤 裏:赤
B 表:青 裏:青
C 表:赤 裏:青
1枚を取って片面を上にして置いたということは、A、B、Cについてそれぞれ上面が表になった場合と裏になった場合があるので、次の6通りのいずれかになります。それぞれの確率は等しいです。
(1) A 表:赤
(2) A 裏:赤
(3) B 表:青
(4) B 裏:青
(5) C 表:赤
(6) C 裏:青
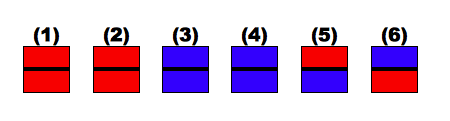
上面が赤になったということは次の3通りのいずれかです。それぞれの確率は等しいです。
(1) A 表:赤 → A 裏:赤
(2) A 裏:赤 → A 表:赤
(5) C 表:赤 → C 裏:青
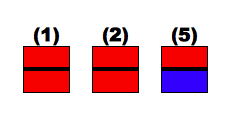
このうち、下面が青になるのは1通りです。
3通りのうち1通りなので確率は1/3となります。
次のようなシミュレーションをしてみました。JavaScriptです。
すると「0.33」という結果が出て正しいことが分かりました。
var cards, zenbu, ao, i, bango, omote_ura;
cards = [
["red", "red"],
["blue", "blue"],
["red", "blue"]
];
zenbu = 0; //赤だった場合の数
ao = 0; //その裏が青だった場合の数
for(i = 0; i < 100000; i++) {
bango = Math.floor(Math.random() * 3);
omote_ura = Math.floor(Math.random() * 2);
if(cards[bango][omote_ura] == "red") {
zenbu++;
if(cards[bango][1 - omote_ura] == "blue") {
ao++;
}
}
}
alert(ao / zenbu);
cards = [
["red", "red"],
["blue", "blue"],
["red", "blue"]
];
zenbu = 0; //赤だった場合の数
ao = 0; //その裏が青だった場合の数
for(i = 0; i < 100000; i++) {
bango = Math.floor(Math.random() * 3);
omote_ura = Math.floor(Math.random() * 2);
if(cards[bango][omote_ura] == "red") {
zenbu++;
if(cards[bango][1 - omote_ura] == "blue") {
ao++;
}
}
}
alert(ao / zenbu);
以前、これと似たような「一人は男と分かっているときのもう一人は?」という記事を書きましたので、参考にしてください。



コメント