3×3のマス目に1から9までの数を重複なく入れ、縦、横、斜めの合計がすべて等しくなるものを魔方陣と言いますが、これを考えてみます。
なお「魔法陣」ではありません。
1から9までの数が重複なく入るということはすべてのマスの合計は1+2+…+9=45となります。
縦、横の合計がすべて等しいということから3個の数からなる1列の合計はどれも15になります。
3個の数の組合せで合計が15になるものを考えます。
1を含む組み合わせは
1-5-9と1-6-8の2通り。
2を含む組み合わせは
2-4-9と2-5-8と2-6-7の3通り。
このようにして挙げると次の通り。
1-5-9、1-6-8、
2-4-9、2-5-8、2-6-7、
3-4-8、3-5-7、
4-2-9、4-3-8、4-5-6、
5-1-9、5-2-8、5-3-7、5-4-6、
6-1-8、6-2-7、6-4-5、
7-2-6、7-3-5、
8-1-6、8-2-5、8-3-4、
9-1-5、9-2-4
ところで真ん中のマスに入る数は何か。
縦、横、右上がり斜め、右下がり斜め、と4つの組合せに共通して使われる数です。
となれば5しかありません。

8 と9 は同じ組(縦、横、斜め)には入りませんので次の2 通りしかありません。
(a)

(b)

(b)の場合は途中で埋められなくなります。
(a)の場合は残りのマスは簡単に埋められます。これが答えで、対称を除けば、一通りしかありません。
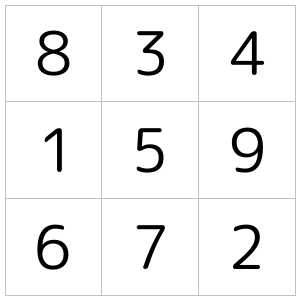
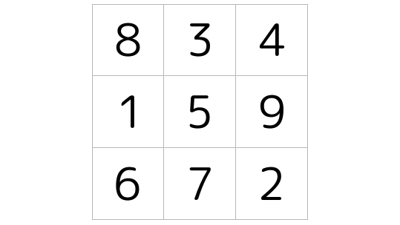


コメント