コサインのマクローリン展開をPythonで
Yahoo!知恵袋にこんな問題がありました。
「次の式の値をPythonで計算せよ。」
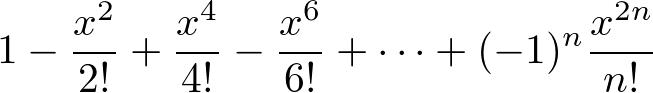
「どこかで見たことがあるぞ」と思い、調べてみると、コサインのマクローリン展開でした。
とりあえずPythonで書いてみます。
元は「xとnの値の入力は対話形式にせよ」というもので「何の意味があるのか」と疑問だったので無視しています。
import matplotlib.pyplot as plt
def main():
n = 20
x = []
y = []
a = range_float(0, 3.14 * 4, 0.1)
for x0 in a:
x.append(x0)
y.append(func(x0, n))
plt.plot(x, y)
plt.show()
def func(x, n):
v = 0
for m in range(0, n + 1):
v += (-1) ** m * x ** (2 * m) / fact(2 * m)
return v
def fact(n):
v = 1
for m in range(1, n + 1):
v *= m
return v
def range_float(start, end, step):
a = []
n = (end - start) / step
for i in range(0, int(n)):
a.append(start + step * i)
return a
if __name__ == '__main__':
main()
def main():
n = 20
x = []
y = []
a = range_float(0, 3.14 * 4, 0.1)
for x0 in a:
x.append(x0)
y.append(func(x0, n))
plt.plot(x, y)
plt.show()
def func(x, n):
v = 0
for m in range(0, n + 1):
v += (-1) ** m * x ** (2 * m) / fact(2 * m)
return v
def fact(n):
v = 1
for m in range(1, n + 1):
v *= m
return v
def range_float(start, end, step):
a = []
n = (end - start) / step
for i in range(0, int(n)):
a.append(start + step * i)
return a
if __name__ == '__main__':
main()
なるべくピュアなPythonで書こうと思い、NumPyなどは使っていません。
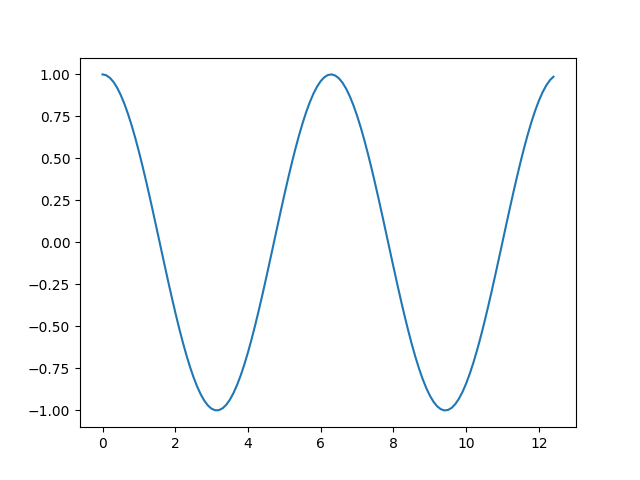
一方でmatplotlibを使って、グラフにしてみました。コサインカーブになることが分かります。
冒頭の式のTexは次のとおりです。
1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots+(-1)^n\frac{x^{2n}}{n!}
これを次のサイトで画像に変換しました。
[ 2021年5月23日 | カテゴリー: Python, デジタル | タグ: Matplotlib , 数学 ]
« Pythonのスクレイピングライブラリ「Helium」の使い方 | Pythonでマージソート »
コメントを残す