こんな問題がありました。
ある数から、1つずつ大きい数を順に足していって2525になる、数の組をすべてあげなさい。
1から10までを足すと55になりますが、このような計算をして2525になるものを見つけよ、というわけです。
簡単なのは「1262から1263まで」です。
また「1から100まで」は5050であり2525はその半分なので「26から75まで」が合いそうです。実際、2525になります。
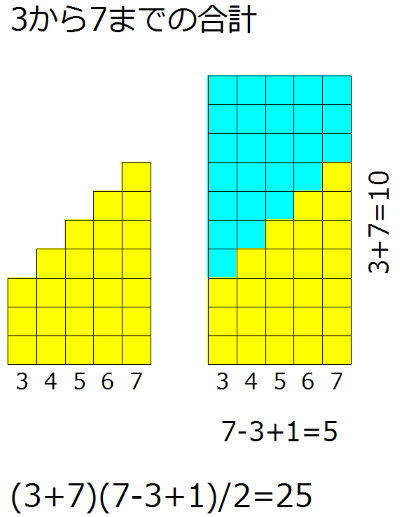
一般に「xからyまで」の合計は
(x+y)(y-x+1)/2
で表せます。ガウスが少年時代に見つけたことで知られます。
これを使って、この問題を解いてみます。
解答
(x+y)(y-x+1)/2=2525
となるx,yを求める。
(x+y)(y-x+1)=5050
となる
a=x+y
b=y-x+1
とする。
ab=5050
となるa,bを求める。
a,bは5050の約数である。またa>bである。したがって
a=5050,b=1
a=2525,b=2
a=1010,b=5
a=505,b=10
a=202,b=25
a=101,b=50
が該当する。
a=x+y
b=y-x+1
から
x=(a-b+1)/2
y=(a+b-1)/2
である。
したがって
x=2525,y=2525
x=1262,y=1263
x=503,y=507
x=248,y=257
x=89,y=113
x=26,y=75
が該当する。これが答えである。
JavaScript
検算のためにJavaScriptで求めてみました。しらみつぶしです。
Just a moment...
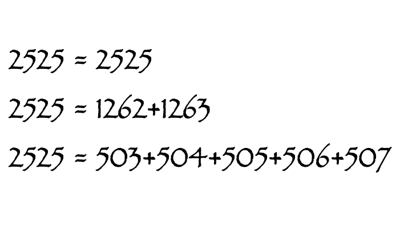


コメント