ネットでこんな問題を見つけました。
Pythonでシンプソンの公式を使って次の式の値を求めよ。
正確な値はπである。
シンプソンの公式を知らなかったので調べてみました。次のページが簡潔で分かりやすかったです。定積分の近似値を求める公式のようです。
区間[a,b]を 2n 等分し,その分点を順に a=x0,x1,x2,…,x2n=b とし,これらに対応する y=f(x)の値をそれぞれ,y0,y1,y2,…,y2n とすれば,定積分 S の近似値は S≅(h/3){y0+4(y1+y3+…+y2n-1)+2(y2+y4+…+y2n-2)+y2n}で与えられる。ただし h=(b-a)/2n である。(コトバンク)
Pythonで書いてみました。
def main():
a = 0
b = 1
n = 1000
print(simpson(f, a, b, n))
def simpson(f, a, b, n):
# s=(h/3){y0+4(y1+...+y2n-1)+2(y2+...+y2n-2)+y2n}
# h=(b-a)/2n
# ya=y1+...+y2n-1
# yb=y2+...+y2n-2
ya = 0
for i in range(1, 2 * n - 1 + 1, 2):
x = (b - a) / (2 * n) * i
ya += f(x)
yb = 0
for i in range(2, 2 * n + 1, 2):
x = (b - a) / (2 * n) * i
yb += f(x)
y0 = f(a)
y2n = f(b)
h = (b - a) / 2 / n
return h / 3 * (f(0) + 4 * ya + 2 * yb + f(y2n))
def f(x):
return 4 / (1 + x ** 2)
if __name__ == '__main__':
main()
a = 0
b = 1
n = 1000
print(simpson(f, a, b, n))
def simpson(f, a, b, n):
# s=(h/3){y0+4(y1+...+y2n-1)+2(y2+...+y2n-2)+y2n}
# h=(b-a)/2n
# ya=y1+...+y2n-1
# yb=y2+...+y2n-2
ya = 0
for i in range(1, 2 * n - 1 + 1, 2):
x = (b - a) / (2 * n) * i
ya += f(x)
yb = 0
for i in range(2, 2 * n + 1, 2):
x = (b - a) / (2 * n) * i
yb += f(x)
y0 = f(a)
y2n = f(b)
h = (b - a) / 2 / n
return h / 3 * (f(0) + 4 * ya + 2 * yb + f(y2n))
def f(x):
return 4 / (1 + x ** 2)
if __name__ == '__main__':
main()
結果は
3.1420593202564566
となりました。

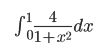


コメント