円錐の表面積の求め方をネットで調べたところ、おかしな説明がいくつも見つかったので自分で整理してみました。
展開図を考えて扇形と円に分解します。次に扇形の面積を求めるのですが中心角を使った説明をしているケースが多いのです。
一般の扇形ならばそれが正しいですが円錐の側面の扇形に限ってはムダです。
円錐の表面積

底面は円、側面は扇形になります。それぞれ求めて加えればいいです。
扇形も円の一部なのでまず円の面積の求め方を考えます。
円の面積
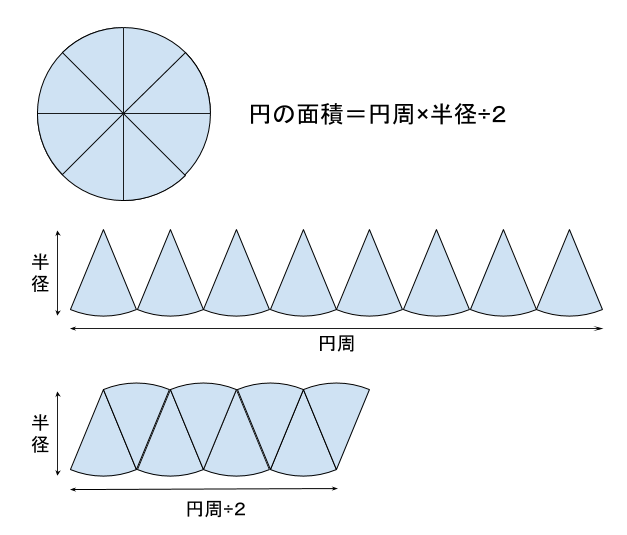
円を多くの扇形に分解します。
これを上の通り横に並べて半分をひっくり返して組み合わせると平行四辺形に近い図形になります。扇形を細かく分解するとほぼ平行四辺形になります。
平行四辺形の面積=底辺×高さ
円の面積=円周÷2×半径
となります。
円周=直径×3.14=半径×2×3.14
なので
円の面積=半径×2×3.14÷2×半径=半径×半径×3.14
となります。
扇形の面積
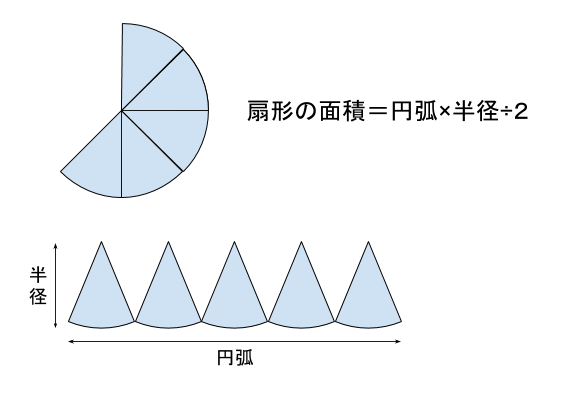
扇形も上の円の面積を同じ求め方ができます。
扇形の面積=円弧÷2×半径
円錐の表面積(まとめ)

底面
底面の面積=半径×半径×3.14
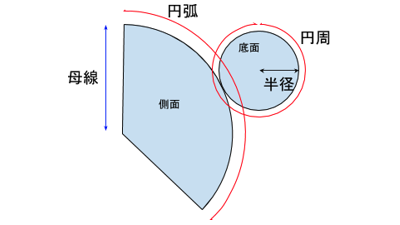
側面
側面の扇形の円弧の長さは底面の円周の長さと同じなります。
円弧=円周=半径×2×3.14
です。
「扇形の面積=円弧÷2×半径」なので
側面の面積=(半径×2×3.14)÷2×(母線)=半径×母線×3.14
となります。
表面積
表面積=底面の面積+側面の面積
表面積=(半径×半径✕3.14)+(半径✕母線✕3.14)
表面積=半径✕(半径+母線)✕3.14
となります。
「中心角」がなくても求められることがポイントです。


コメント