階段を1段または2段ずつ上る方法は何通りか

Pocket

フィボナッチ数とは、1番目は「1」、2番目は「2」、3番目は「3」、4番目は「5」、5番目は「8」のように、1番目と2番目を足すと3番目、2番目と3番目を足すと4番目という関係になっている数です。
次のような面白い性質があります。

階段を1段または2段ずつ上る方法は何通りかを数えるとフィボナッチ数になる。

例えば3段の階段は「1段ずつ3回上る」「2段上って1段上る」「1段上って3段上る」の3通りがあります。
各段数の上がる方法を数えるとフィボナッチ数になるというのです。

とりあえず数えてみる

「1段ずつ3回上る」を「1+1+1」、「2段上って1段上る」を「2+1」と表わすことにする。

1段の階段

1段上り1回、1通り。
1

2段の階段

1段上り2回と2段上り1回、2通り。
1+1
2

3段の階段

次の3通り。
1+1+1
2+1
1+2

4段の階段

次の5通り。
1+1+1+1
2+1+1
1+2+1
1+1+2
2+2

5段の階段

1段上り5回、1通り。
1+1+1+1+1
2段上り1回と1段上り3回、4通り。
2+1+1+1
1+2+1+1
1+1+2+1
1+1+1+2
2段上り2回と1段上り1回、3通り。
2+2+1
2+1+2
1+2+2
全部で8通り。

6段の階段

1段上り6回、1通り。
1+1+1+1+1+1
2段上り1回と1段上り4回、次の5通り。
2+1+1+1+1
1+2+1+1+1
1+1+2+1+1
1+1+1+2+1
1+1+1+1+2
2段上り2回と1段上り2回、次の6通り。
2+2+1+1
2+1+2+1
2+1+1+2
1+2+2+1
1+2+1+2
1+1+2+2
2段上り3回、次の1通り。
2+2+2
全部で13通り。

7段の階段

1段上り7回。
1通り。

2段上り1回と1段上り5回。
全部で6回のうちどこで2段上りするか、つまり6個から1個とる組合せ。
6通り。

2段上り2回と1段上り3回。
全部で5回のうちどの2回で2段上りするか、つまり5個から2個とる組合せ。
(5*4)/(2*1)=10通り。

2段上り3回と1段上り1回。
全部で4回のうちどの3回で2段上りするか、つまり4個から3個とる組合せ。
(4*3*2)/(3*2*1)=4通り。

全部で21通り。

フィボナッチ数になっているか

ここまでまとめると次の通り。

1段 1通り
2段 2通り
3段 3通り
4段 5通り
5段 8通り
6段 13通り
7段 21通り

確かにフィボナッチ数になっている。この関係がこの先も続くかを調べる。

帰納法を使って証明

「X(n)=X(n-1)+X(n-2)の関係が成り立つ」
ときに
「X(n+1)=X(n)+X(n-1)の関係が成り立つ」
ことを示す。

(n+1)段に上るためには
(a)(n-1)段目から上る。
(b)n段目から上る。
の二つの方法が考えられる。

(a)(n-1)段目から上る
(n-1)段目まではX(n-1)通り。
残り2段なので、1段上り2回、2段上り1回の2通り。

(b)n段目から上る
n段に上るためには
(c)(n-2)段目から上る。
(d)(n-1)段目から上る。
の二つの方法が考えられるが、(a)と重複しない方法は
(e)(n-2)段目から2段上る。
の一つの方法。
(n-2)段目まではX(n-2)通り。
残り1段なので、1段上り1回の1通り。

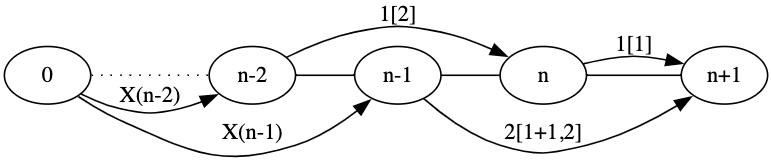
(a)と(b)を合わせると
X(n+1)=X(n-1)+X(n-1)+X(n-2)
X(n+1)=X(n-1)+{X(n-1)+X(n-2)}
X(n+1)=X(n-1)+X(n)
X(n+1)=X(n)+X(n-1)
よって示せた。

X(3)=X(2)+X(1)が成り立つのは上で確認済み。
したがって、全てのnについて「X(n)=X(n-1)+X(n-2)の関係が成り立つ」と言える。

[ 2014年3月18日 | カテゴリー: 小ネタ | タグ: フィボナッチ数 , 数学 , 証明 ]

« Macでテキストを音声ファイルに変換する方法 | 1000本から毒入りワインを見つける問題 »

You Look Too Cool