2018年は2つの素数の2乗の和、70年間で今年だけ!
こんな記事がありました。
「2017は3つの素数の3乗の和、400年間で今年だけ!」 父から送られてきた年賀状に数学クラスタが沸く - ねとらぼ
この年賀状によると「2017」は3つの素数の3乗の和(7^3+7^3+11^3=2017)になるとのこと。3つの素数の3乗の和になる数字は少ない方から数えて30番目となりますが、29番目は「1799(5^3+7^3+11^3=1799)」で31番目は「2213(2^3+2^3+13^3=2213)」となるそうです。
よく見つけたなあ、と感心します。
ちょっと先取りして2018年について同じようなことを確認してみました。
上の記事にあるように2018は「3つの素数の3乗の和」にはなりません。
では2018は「2つの素数の2乗の和」になるか。
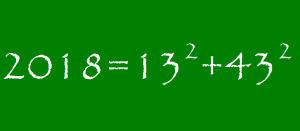
なるんですねえ!
2018=13^2+43^2
となります。
この一つ前は
1970=11^2+43^2または1970=17^2+41^2
であり、一つ後は
2042=19^2+41^2
となります。
「2018年は2つの素数の2乗の和であり、このような年は70年間で今年だけ」と言えます。
「3つの素数の3乗の和」については上述の通りです。
ついでに「4つの素数の4乗の和」について調べてみると次のようになりました。
1956=3^4+5^4+5^4+5^4
2449=2^4+2^4+2^4+7^4
次にこのような年になるのは2449年です。
最後に「○つの素数の○乗の和」となる1500から2499までについて列挙しておきます。
2つの素数の2乗の和
1538=13^2+37^2
1658=17^2+37^2
1682=29^2+29^2
1685=2^2+41^2
1690=3^2+41^2
1706=5^2+41^2
1730=19^2+37^2
1730=7^2+41^2
1802=11^2+41^2
1802=29^2+31^2
1850=13^2+41^2
1853=2^2+43^2
1858=3^2+43^2
1874=5^2+43^2
1898=23^2+37^2
1898=7^2+43^2
1922=31^2+31^2
1970=11^2+43^2
1970=17^2+41^2
2018=13^2+43^2
2042=19^2+41^2
2138=17^2+43^2
2210=23^2+41^2
2210=19^2+43^2
2210=29^2+37^2
2213=2^2+47^2
2218=3^2+47^2
2234=5^2+47^2
2258=7^2+47^2
2330=11^2+47^2
2330=31^2+37^2
2378=23^2+43^2
2378=13^2+47^2
2498=17^2+47^2
3つの素数の3乗の和
1581=5^3+5^3+11^3
1682=2^3+7^3+11^3
1701=3^3+7^3+11^3
1799=5^3+7^3+11^3
2017=7^3+7^3+11^3
2213=2^3+2^3+13^3
2232=2^3+3^3+13^3
2251=3^3+3^3+13^3
2330=2^3+5^3+13^3
2349=3^3+5^3+13^3
2447=5^3+5^3+13^3
4つの素数の4乗の和
1891=2^4+5^4+5^4+5^4
1956=3^4+5^4+5^4+5^4
2449=2^4+2^4+2^4+7^4
[ 2017年1月8日 | カテゴリー: 豆知識 | タグ: 数学 , 素数 ]
« JavaScriptで素数を列挙する | 中村麺三郎商店 »
コメントを残す