陸上トラックの面積を最大にする問題
こんな問題がありました。
400mの陸上トラック(両端が半円で、半円の間を80m以上の直線が結ぶ形)を作りなさい。
陸上トラックの中の面積を最大にするには、どのような設計にすればいいか。(Yahoo!知恵袋)
いくつか、答えが書かれていますが、どれも答えになっていない気がします。
自分で解いてみました。
直線部分の長さをx、半円部分の半径をyとする。
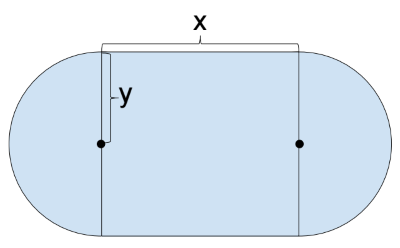
半円部分の弧の長さは2πy/2=πyとなる。両側で2πyとなる。
直線部分の長さはx、両側で2xとなる。
周の長さは2x+2πyとなり、これが400メートルであるから、2x+2πy=400からy=(200-x)/πとなる。…(1)
トラックは半円+長方形+半円なので円+長方形で求められる。
面積をSとするとS=πy^2+2xyとなる。
(1)からS=π((200-x)/π)^2+2x(200-x)/πとなり、これを計算するとS=(40000-x^2)/πとなる。
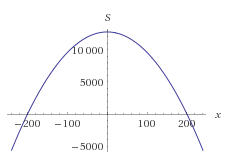
グラフにすると下に示すように上が凸の二次曲線なのでx=0のときSは最大になる(つまり直線部分がない円の場合)。
しかし問題文からx>=80なのでx=80のときSは最大になる。このときy=120/πになる。
答えは「半径120/πメートルの半円と80メートルの直線を組み合わせたトラック」となる。
[ 2016年9月3日 | カテゴリー: 小ネタ | タグ: 数学 ]
« SVGをPNGに変換するツール(まとめ) | 1日の予定を円グラフ風に表示する「24時間サークルメーカー」 »
コメントを残す